B-Trees
Overview
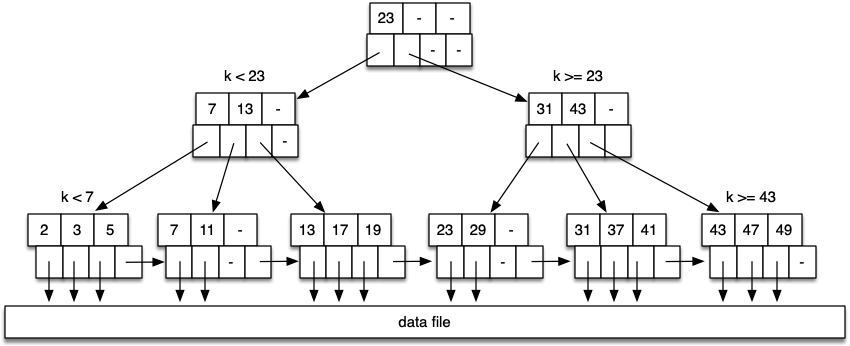
B-Trees are multi-way search trees with properties:
- Remains balanced after updates.
- Each node has at least
(n - 1) / 2entries in it. - Each tree node occupies an entire disk page.
B-Trees are better than general multi-way search trees:
- Better storage utilisation.
- Better worst case performance.
Selection with B-Trees
One Queries
def find(key, tree) -> Node:
return search(key, root_of(tree))
def search(key, node: Node) -> Node:
if is_leaf(node):
return node
keys = # array of nk key values in node
pages = # array of nk + 1 ptrs to child nodes
if key <= keys[0]:
return search(key, pages[0])
elif k > keys[nk - 1]:
return search(key, pages[nk])
else:
for i in range(0, nk):
if keys[i] < keys <= keys[i + 1]:
return search(key, pages[i + 1])
Cost_one = (D + 1)_r
Range Queries
lowNode = find(lowKey, tree)
curNode = lowNode
while curNode.val <= highKey:
# add pageOf(tid) to Pages to be scanned
# each curNode has pointer to immediately right neighbour on same level
curNode = curNode.next
# scan Pages looking for matching tuples
Cost_range = (D + b_i + b_q)_r.
Insertion
Overview of method:
- Find leaf node and position in node where new key belongs.
- If node is not full, insert entry into appropriate position.
- If node is full:
- Promote middle element to parent.
- Split node into two half full-nodes (< middle, >= middle).
- Insert new key into appropriate half-full node.
- If parent full, split and promote upwards.
- If reach root, and root is full, make new root upwards.
Insertion Cost
Cost_insert = Cost_treeSearch + Cost_treeInsert + Cost_dataInsert.
Best case: write one page (most of time).
- Traverse from root to leaf.
- Read/write data page, write updated leaf.
Cost_insert = D_r + 1_w + 1_r + 1_w
Common case: 3 node writes (rearrange 2 leaves + parent).
- Traverse from root to leaf, holding nodes in buffer.
- Read/write data page.
- Update/write leaf, parent and sibling.
Cost_insert = D_r + 3_w + 1_r + 1_w.
Worst case: propagate to root.
- Traverse from root to leaf.
- Read/write data page.
- Update/write leaf, parent and sibling.
- Repeat previous step
(D - 1)times. Cost_insert = D_r + D * 3_w + 1_r + 1_w.