Multi-Dimensional Hashing
Hashing and PMR
For a PMR query like:
select * from R where a_1 = C_1 and ... a_n = C_n
- If one
a_iis the hash key, query is very efficient. - If no
a_iis the hash key, need to use linear search.
Can be alleviated using multi-attribute hashing (MAH).
- Form a composite hash value involving all attributes.
- At query time, some components of composite hash are known.
- Allows us to limit number of data pages needed to be checked.
- For unknown components, generate all possibilities for pages.
MAH works in conjunction with any dynamic hashing scheme.
Hashing Parameters
- File size:
b = 2^dpages. So used-bit hash values. - Relation has
nattributes:a_1, a_2, ... , a_n. - Attribute
a_ihas hash functionh_i. - Attribute
a_icontributesd_ibits to the combined hash value. - Total bits:
d = sum(d_i for i=1..=n). - Choice vector specifies for all
k in 0..=d - 1bitjfromh_i(a_i)contributes bitkin combined hash value.

MA.Hashing Example
Consider relation:
Deposit(branch, acctNo, name, amount)
Assume 8 main data pages (plus overflows) with the hash parameters:
d = 3, d_1 = 1, d_2 = 1, d_3 = 1, d_4 = 0.- Attribute 4 (
amount) is ignored as we assume we never do equality conditions on this field.
- Attribute 4 (
Choice vector:

- Bit 0 in hash comes from bit 0 of
h_1(a_1). - Bit 1 in hash comes from bit 0 of
h_2(a_2). - Etc.
Consider the tuple:
| branch | acctNo | name | amount |
|---|---|---|---|
| Downtown | 101 | Johnston | 512 |

Hash Function Implementation
HashVal = # unsigned int
@dataclass
class CVElem:
attr: int
bit: int
ChoiceVec = List[CVElem]
ith_bit = lambda i, val: # get ith bit from val
def hash(t: Tuple, cv: ChoiceVec, d: int) -> HashVal:
hashed_attributes: HashVal = # list of size nattr(t).
res: HashVal = 0
for i in range(1, nAttr(t) + 1):
hashed_attributes[i] = hash_any(attrVal(t, i))
for i in range(0, d):
a = cv[i].attr
b = cv[i].bit
res = res | (ith_bit(i=b, val=hashed_attributes[a]) << i)
return res
Queries with MAH
In a partial match query:
- Values of some attributes are known.
- Values of other attributes are unknown.
Consider query:
select amount from Deposit where name='Green'
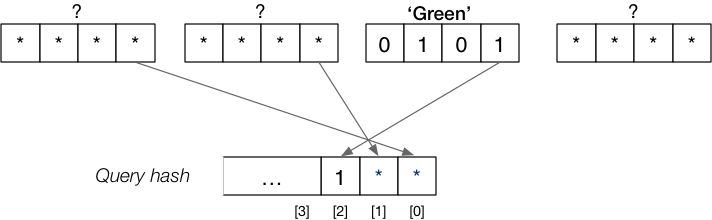
Matching tuples must be in pages: 100, 101, 110 or 111.
Query Algorithm
def partialHash(q: Query) -> Tuple[int, int]:
numStars = 0
for i in q.attributes:
if hasValue(q, i):
# set d[i] bits in composite hash using choice vector and hash(q, i).
else:
# set d[i] *'s in composite hash using choice vector
numStars += d[i]
return d, numStars
def findTuples(r: Relation, q: Query) -> Set[Tuple]:
results = set()
compositeHash, numStars = partialHash(q)
for i in range(0, 2 ** numStars):
filledCompositeHash = # replace *'s in compositeHash using i and choice vector.
buf = getPage(fileOf(r), filledCompositeHash)
for t in buf:
if satisfiesQuery(t, q):
results.add(t)
return results
Query Cost
Cost(Q) = 2^s where s is the number of stars (attributes not appearing in the query).
Query distribution gives probability p_Q of asking each query type Q.
Min query cost occurs when all attributes are used in query:
Cost_min,pmr = 1.
Max query occurs when no attributes are specified:
Cost_max,pmr = 2^d = b.
Average cost is given by weighted sum over all query types:
Optimising MA.Hashing Cost
For a given application, useful to minimise Cost_pmr. Can be achieved by choosing appropriate values for d_i (choice vector).
Heuristics:
- Distribution of query types (more bits to frequently used attributes).
- Size of attribute domain (<= bits to represent all values in domain).
- Discriminatory power (more bits to highly discriminating attributes).
Trade-off: making Q_j more efficient makes Q_k less efficient.
This is a combinatorial optimisation problem.