Multi-dimensional Tree Indexes
Overview
Suppose we have the tuples:
R('a',1) R('a',5) R('b',2) R('d',1)
R('d',2) R('d',4) R('d',8) R('g',3)
R('j',7) R('m',1) R('r',5) R('z',9)
The tuple-space for the tuples is given by:

Different multi-dimensional search trees partition the tuple-space in different ways.
kd-Trees
kd-trees are multi-way search trees where:
- Each level of the tree partitions on a different attribute.
- Each node contains
n - 1key values, points tonsubtrees.
Example partitioning:

Corresponding tree:
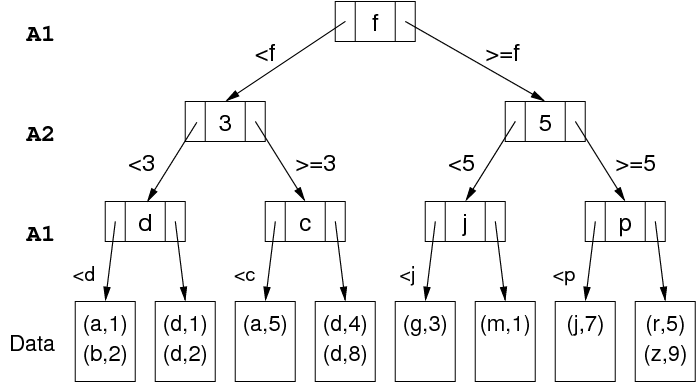
Note: tree in image is binary and hence has n = 2.
Searching in kd-Trees
def search(q: Query, r: Relation, l: Level, n: Node) -> Node:
if isDataPage(n):
buf = getPage(fileOf(R), idOf(n)):
# check buf for matching tuples
# return matching tuples
else:
a = attributeLevel[l]
if not hasValue(q, a)
nextNodes = # all children of n
else:
val = getAttribute(q, a)
nextNodes = find(n, q, a, val)
for child in nextNodes:
search(q, r, l + 1, child)
Quad Trees
Quad trees use regular, disjoint partitioning of tuple space:
- For 2d, partition space into quadrants (NW, NE, SW, SE).
- Each quadrant can be further subdivided into four, etc.
Example partitioning:
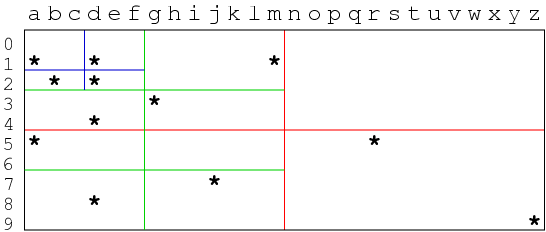
Corresponding tree:

Basis for partitioning:
- Quadrant that has no sub-partitions is a leaf quadrant.
- Each leaf quadrant maps to a single data page.
- Subdivide until points in each quadrant fit into one data page.
- Ideal: same number of points in each leaf quadrant (balanced).
- Point density varies over space.
- Different regions require different levels of partitioning.
- Means tree is not necessarily balanced.
Searching in Quad Trees
- Find all regions in current node that query overlaps with.
- For each region, check its node.
- If node is a leaf, check corresponding page for matches.
- Else recursively repeat search from current node.
R-Trees
R-Trees use a flexible, overlapping partitioning of tuple space:
- Each node in the tree represents a kd hypercube.
- Its children represent (possibly overlapping) subregions.
- The child regions do not need to cover the entire parent region.
Overlap and partial cover means:
- Can optimise space partitioning wrt. data distribution.
- So that there are similar number of points in each region.
Aim: height-balanced, partly-full index pages.
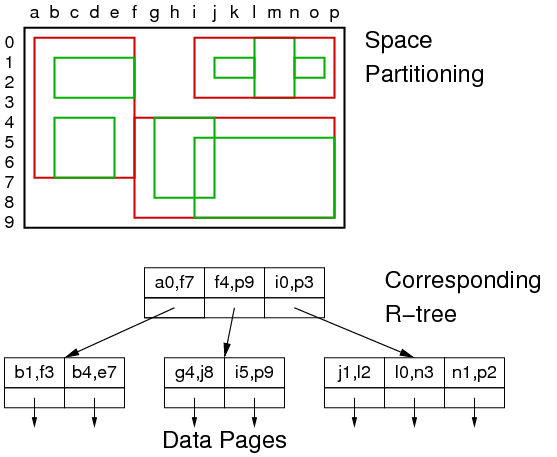
Insertion into R-tree
Insertion of an object R occurs as follows:
- Start at root, look for children that completely contain
R. - If no child completely contains
R, choose one of the children and expand its boundaries so that it does containR. - If several children contain
R, choose one and proceed to child. - Repeat above containment search in children of current node.
- Once we reach data page, insert
Rif there is room. - If no room in data page, replace by two data pages.
- Partition existing objects between two data pages.
- Update node pointing to data pages.
- May cause B-tree-like propagation of node changes up into tree.
Query with R-trees
Designed to handle space queries and “where-am-I” queries.
“Where-am-I” query: find all regions containing a given point P:
- Start at root, select all children whose subregions contain
P. - If there are zero such regions, search finishes with
Pnot found. - Otherwise, recursively search within node for each subregion.
- Once we reach a leaf, we know that region contains
P.
Space (region) queries are handled in a similar way:
- Traverse down any path that intersects the query region.
Costs of Search in Multi-d Trees
Best case: PMR query where all attributes have known values:
- In kd-trees and quad-trees, follow single tree path.
- Cost is equal to depth
Dof tree. - In R-trees, may follow several paths (overlapping partitions).
Typical case: some attributes are unknown or defined by range:
- Need to visit multiple sub-trees.
- How many depends on: range, choice-points in tree nodes.
Multi-Dimensional Trees in PostgreSQL
PostgreSQL uses Generalized Search Trees (GiST).
GiST indexes parameterise: data type, searching, splitting:
- Via seven user-defined functions.
GiST trees have the following structural constraints:
- Every node is at least fraction
ffull (e.g. 0.5). - The root node has at least two children (unless also a leaf).
- All leaves appear at the same level.