Indexing Overview
Definition
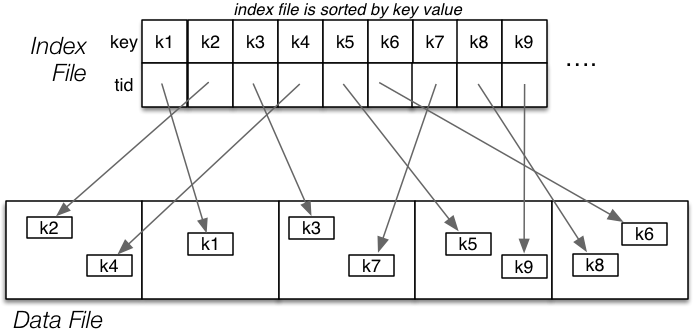
An index is a file of (keyVal, tupleID) pairs, e.g.
Types of Indexes
A 1d index is based on the value of a single attribute A.
Some possible properties of A:
- May be used to sort data file (or may be sorted on some other field).
- Values may be unique (or there may be multiple instances).
Taxonomy of index types, based on properties of index attribute:
- Primary: index on unique field, data file may be sorted on
A. - Clustering: index on non-unique field, data file sorted on
A. - Secondary: file not sorted on
A.
A given table may have indexes on several attributes.
Index Structures
Indexes may be structured in several ways:
- Dense: every tuple is referenced by an index entry.
- Sparse: only some tuples are referenced by index entries.
- Single-level: tuples are accessed directly from index file.
- Multi-level: may need to access several pages to reach tuple.
Selection with Primary Index
Note: data file might not be ordered, index files are always ordered.
One Queries
ix = # binary search index for entry with key K
if: #nothing found
return NotFound
b = getPage(pageOf(ix.tid))
t = getTuple(b, offsetOf(tx.tid)) # may require reading overflow pages
return t
Worst case: read log_2(i) index pages + read 1 + Ov data pages.
Thus, Cost_one,prim = log_2(i) + 1 + Ov.
Range Queries
For range queries on primary key:
- Use index search to find lower bound.
- Read index sequentially until reach upper bound.
- Accumulate set of buckets to be examined.
- Examine each bucket in turn to check for matches.
For queries not involving primary key, index gives no help.
Algorithm when data file is not sorted:
# E.g. select * from R where a between low and high
pages = {}
results = {}
ixPage = findIndexPage(R.ixf, low)
while ixTuple := getNextIndexTuple(R.ixf):
if ixTup.key > high:
break
pages = pages.union(pageOf(ix.Tup.tid))
for pid in pages:
while buf = getPage(R.datf, pid):
for t in buf:
if low <= t.a and t.a <= high:
results = results.add(t)
return results
Partial Match Retrieval (PMR) Queries
For PMR queries involving primary key:
- Search as if performing one query.
For queries not involving primary key, index gives no help.
Insertion with Primary Index
Overview:
tid = # insert tuple into page P at position p
# find location for new index entry (k, tid) into index file
Problem: order of index entries must be maintained:
- Need to avoid overflow pages in index.
- So, reorganise index file by moving entries down.
Reorganisation requires, on average, read/write half of index file:
Cost_insert,prim = (log_2(i))_r + i / 2 * (1_r + 1_w) + (1 + Ov)_r + (1 + δ)_w.
Deletion with Primary Index
Overview:
# find tuple using index
# mark tuple as deleted
# delete index entry for tuple
If we delete index entries by marking:
Cost_delete,prim = (log_2(i))_r + (1 + Ov)_R + 1_w + 1_w.
If we delete index entry by file reorganisation:
Cost_delete,prim = (log_2(i)) + (1 + Ov)_R + i / 2 * (1_r + 1_w) + 1_w.
Clustering Index
Data file sorted: can use one index entry for each unique key value.

Cost penalty: maintaining both index and data file as sorted.
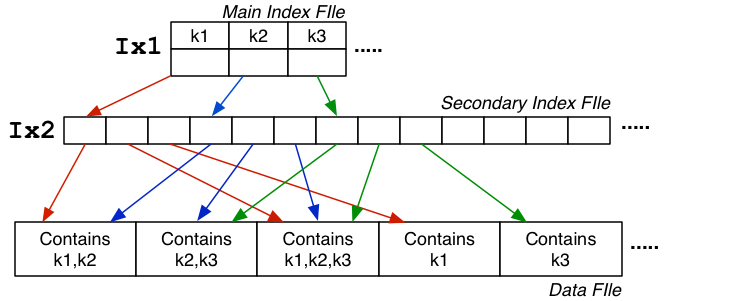
Secondary Index
Data file not sorted: want one index entry for each key value.
Cost_pmr = (log_2(i)_ix1 + a_ix2 + b_q * (1 + Ov))
Multi-level Indexes
Secondary index used two index files to speed up search:
- By keeping the initial index search relatively quick.
ix1is small (depends on number of unique key values).ix2is large (depends on amount of repetition of keys).- Typically
b_ix1 << b_ix2 << b.
Could improve further by:
- Making
ix1sparse, sinceix2is guaranteed to be ordered. - In this case:
b_ix1 = ceil(b_ix2 / c_i). - If
ix1becomes too large, addix3and makeix2sparse. - If data file ordered on key, could make
ix3sparse.
Ultimately, reduce top-level of index hierarchy to one page.

Algorithm for one queries:
xpid = # top level index page
for level in range(1, d + 1):
# read index entry xpid
# search index page for Jth entry where index[J].key <= K <= index[J + 1].key
if J == -1:
return NotFound
xpid = index[J].page
pid = xpid
# search page pid and its overflow pages
Cost_one,mli = (d + 1 + Ov)_r.
Note that d = ceil(log_ci(r)) and c_i is large because index entries are small.