Nested-Loop Join
Basic Strategy
For the relational operation Join[a=b](R, S):
result = set()
for pageR in R:
for pageS in S:
for tupleR, tupleS in cartesianProduct(pageR, pageS):
if tupleR.a == tupleS.b:
newTuple = concat(tupleR, tupleS)
result = result.union(newTuple)
Needs input buffers for R and S and output buffer for joined tuples.
Cost = b_R * b_S (without buffering).
Block Nested Loop Join
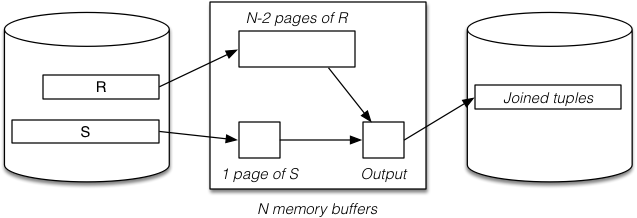
Method (with N memory buffers):
- Read
N - 2page chunks ofRinto memory buffers. - For each page of
S:- Check join condition on all
(t_r, t_s)pairs in buffers.
- Check join condition on all
- Repeat for all
N - 2page chunks ofR.
Cost analysis:
- Best case:
b_R <= N - 2.- Read
b_Rpages of relationRinto buffers. - While whole
Ris buffered, readb_Spages ofS. - Cost =
b_R + b_S.
- Read
- Typical case:
b_R > N - 2.- Read
ceil(b_r / (n - 2))chunks of pages fromR. - For each chunk, read
b_Spages ofS. - Cost =
b_R + b_S * ceil(b_R / (N - 2)).
- Read
Note: always requires r_R * r_S checks of the join condition.
Index Nested Loop Join
Problem with nested-loop join:
- Needs repeated scans of entire inner relation
S.
If there is an index on S, we can avoid such repeated scanning. Consider Join[i=j](R, S):
for tupleR in R:
# use index to select tuples from S where s.j = r.i
for s in selectedTuples(S):
# add (r, s) to result
This method requires:
- One scan of
Rrelation (b_R):- Only one buffer needed, since we use
Rtuple-at-a-time.
- Only one buffer needed, since we use
- For each tuple in
R(r_R), one index lookup onS.- Cost depends on type of index and number of results.
- Best case is when each
R.imatches fewStuples.
Cost = b_R + r_R * Sel_S where Sel_S is the cost of performing a select on S.
Typically Sel_S =
- 1 or 2 for hashing.
b_qfor unclustered index.
Tradeoff: r_R * Sel_S vs b_R * b_S where b_R << r_R and Sel_S << b_s.