Linear Hashing
Overview
Linear Hashing uses a systematic method of growing data file:
- Hash function adapts to changing address range (via
spandd). - Systematic splitting controls length of overflow chains.
Advantage: does not require auxiliary storage for directory. Disadvantage: requires overflow pages (doesn’t split on full pages).
Method
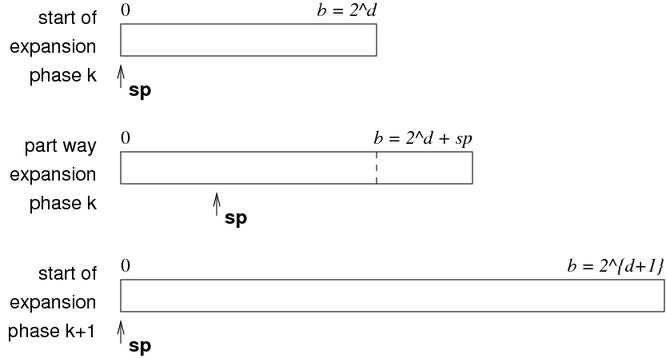
File grows linearly (one page at a time, at regular intervals). Has phases of expansion; over each phase, b doubles.
Selection with Linear Hashing
Power of 2 Case
If b is a power of 2, the file behaves exactly like standard hashing. The d bits of the hash are used to compute the page address.
# select * from R where k = val
h = hash(val)
P = bits(d, h) # lower order bits
for t in P
if t.k == val:
return t
for t in overflowPages(P):
if t.k == val:
return t
Average Cost_one = 1 + Ov.
Non-Power of 2 Case
If b is not a power of 2, treat different parts of the file different.

Parts A and C are treated as if part of a file of size 2^(d + 1). Part B is treated as if part of a file of size 2^d. Part D does not yet exist (tuples in B may eventually move into it).
h = hash(val)
pid = bits(d, h)
# only change is to use more bits if page is before split pointer
if pid < sp:
pid - bits(d + 1, h)
for t in P
if t.k == val:
return t
for t in overflowPages(P):
if t.k == val:
return t

Insertion with Linear Hashing
pid = bits(d, hash(val))
if pid < sp:
pid = bits(d + 1, hash(val))
P = getPage(f, pid)
for page in bucket(P):
if space in page:
page.insert(newTuple)
break
if not insertion:
newOverflowPage = addNewOverflowPage(P)
newOverflowPage.insert(newTuple)
if needSplit:
# partition tuples from bucket sp into buckets sp and sp + 2^d
sp += 1
if isPowerOf2(sp):
d += 1
sp = 0
Splitting
Two approaches to triggering a split:
- Split every time a tuple is inserted into full page.
- Split when load factor reaches threshold (every
kinserts).
Note: always split page sp, even if not full or “current”.
Systematic splitting:
- Eventually reduces length of every overflow chain.
- Helps to maintain short average overflow chain length.
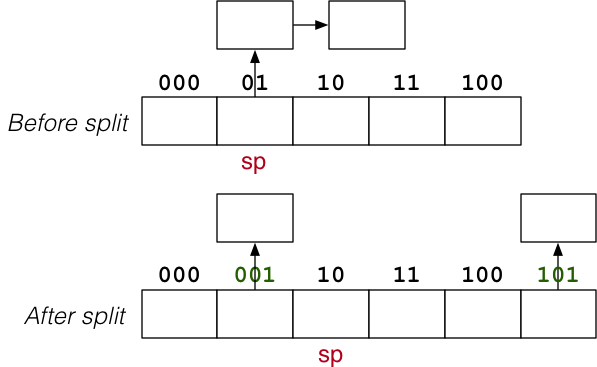
newsp = sp + 2 ** d
oldsp = sp
for t in P[oldsp] and overFlowPages(P[oldsp]):
p = bits(d + 1, hash(t.k))
if p == newp:
bucket[newsp].add(t)
else:
bucket[oldsp].add(t)
sp += 1
if isPowerOf2(sp):
d += 1
sp = 0
Insertion Cost
If no split required, same as standard hashing:
Cost_insert:Best:1_r + 1_w, Average:(1 + Ov)_r + 1w, Worst:(1 + max(Ov))_r + 2_W.
If split occurs, incurs Cost_insert plus cost of splitting:
- Read page
sp(plus all of its overflow pages). - Write page
sp(and its new overflow pages). - Write page
sp + 2^d(and its new overflow pages).
On average, Cost_split = (1 + Ov)_r + (2 + Ov)_w.
Deletion with Linear Hashing
Deletion is similar to ordinary static hash file. BUt might wish to contract file when enough tuples removed.
Method:
- Remove last bucket in data file (contracts linearly).
- Merge tuples from bucket with its buddy page (using
d - 1hash bits).