Projection
Projection Operation
Tuple projTuple(AttrList, Tuple)
- First argument is list of attributes.
- Second argument is a tuple containing those attributes (and more).
- Return value is a new tuple containing only those attributes.
Implementation Without DISTINCT
# attrs = [attr1, attr2, ...]
for page in pages(rel):
for _tuple in tuples(page):
projected_tuple = projTuple(attrs, T)
if (outBuf is full):
# write ouput and clear
outBuf.append(projected_tuple)
if nTuples(outBuf) > 0:
# write output
Implementation With DISTINCT
With DISTINCT, the projection operation needs to:
- Scan entire relation as input.
- Create output tuples containing only requested attributes.
- Implementation depends on tuple internal structure.
- Essentially, make a new tuple with fewer attributes and where the values may be computed from existing attributes.
- Eliminate any duplicates produced.
- Through sorting or hashing.
Sort-based Projection

Requires a temporary file/relation:
# note: can contain multiple pages.
for _tuple in relFile:
projected_tuple = projTuple(attribute_list, _tuple)
tempFile.add(projected_tuple)
tempFile.sort_on(attribute_list)
# note: can contain multiple pages.
for _tuple in tempFile:
if _tuple == previous_tuple:
continue
# write _tuple to result
prev = _tuple
Cost of Sort-based Projection
Costs involved are (assuming B = n + 1 buffers for sort):
- Scanning original relation
Rel:b_R(withc_R). - Writing
Temprelation:b_T(smaller tuples,c_T > c_R, sorted). - Sorting
Temprelation:2 * b_T * ceil(log_n(b_0))whereb_0 = ceil(b_T / B). - Scanning
Temp, removing duplicates:b_T. - Writing the result relation
b_Out(maybe less tuples).
Total cost = b_R + b_T + 2 * b_T * ceil(log_n(b_0)) + b_T + b_Out.
Hash-based Projection
Partitioning phase:
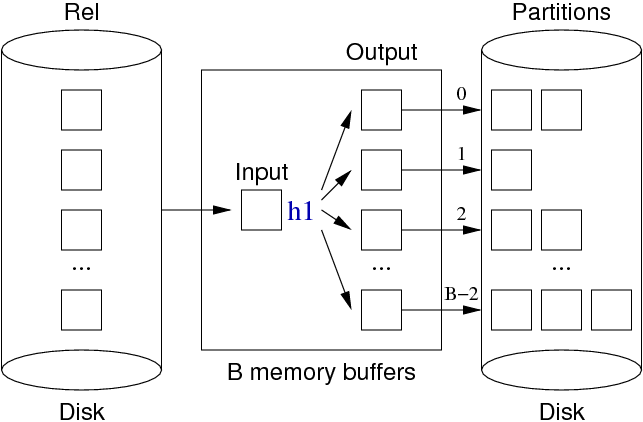
- Each tuple is hashed and placed into separate buckets by hash value.
- Duplicate values will always belong in the same hash bucket, but not necessarily adjacent to each other.
Duplicate elimination phase:

- Each of the previous hash buckets is processed one at a time.
- Each tuple in a hash bucket is rehashed and written to an output buffer if it does not already exist in that output buffer.
Algorithm for both phases:
for _tuple in tuples(rel):
projected_tuple = projTuple(attribute_list, _tuple)
hashed_value = h1(projected_tuple)
B = buffer_for(hashed_value)
if B is full:
# write and clear B
B.insert(projected_tuple)
# note: each partition may contain multiple pages
# all pages for one partition are processed as one
for partition in partitions:
for _tuple in partition:
hashed_value = h2(_tuple)
B = buffer_for(hashed_value)
if _tuple not in B:
B.insert(T)
# write and clear all buffers
Cost of Hash-based Projection
Total consist is sum of:
- Scanning original relation
R:b_R. - Writing partitions:
b_P. - Re-reading partitions:
b_P. - Writing result relation:
b_Out
Total cost = b_R + 2b_P + b_Out.
To ensure that n is larger than the largest partition:
- Use has functions with uniform spread.
- Allocate at least
sqrt(b_r) + 1buffers. - If insufficient buffers, significant re-reading overhead.
Projection on Primary Key
No duplicates, so simple approach works.
Index-only Projection
Can do projection without accessing data file if and only if:
- Relation is indexed on
(A_1, ..., A_n). - Projected attributes are a prefix of
(A_1, ..., A_n).
Basic idea:
- Scan through index file (which is already sorted on attributes).
- Duplicates are already adjacent in index, so easy to skip.
Cost analysis:
- Index has
b_ipages (whereb_i << b_R). - Cost =
b_ireads +b_Outwrites.
Comparison of Projection Methods
Difficult to compare due to different assumptions made:
- Index-only: needs an appropriate index.
- Hash-based: needs buffers and good hash functions.
- Sort-based: needs only buffers.
- This is the default.
Best case scenario for each (assuming n + 1 buffers):
- Index-only:
b_i + b_Out << b_R + b_Out. - Hash-only:
b_R + 2 * b_P + b_Out. - Sort-based:
b_R + b_T + 2 * b_T * ceil(log_n(b_0)) + b_T + b_Out.
Projection in PostgreSQL
Types:
ProjectionInfo { type, pi_state, pi_exprContext }.ExprState { tag, flags, resnull, resvalue, ... }
Functions:
ExecProject(projInfo,...).check_sql_fn_retval(...)